Machine Learning (see the differences  between AI/ML/DL) for real-world applications of AI is extremely challenging.

The process of digital transformation will be supported by cyber-physical systems enabled by advances in statistical machine learning, the availability of Big Data, and increasing computing power. For certain tasks, algorithms achieve performance that exceeds human levels. The challenge is to leverage multimodal information fusion, i.e., integrating data from multiple sources (sensor data, images, *omics) and explaining to an expert why a particular result was achieved. Machine learning models often respond to even small changes, and perturbations can have dramatic effects on the outcome. Therefore, the use of AI in areas of importance to human life (agriculture, forestry, climate, health, etc.) has led to increased demand for trustworthy AI with two main components: Explainability and Robustness. One step to make AI more robust is to leverage expert knowledge. For example, the forester in the loop can often bring experience, expertise, and conceptual understanding to the AI pipeline. Such approaches are not only a solution from a legal perspective, but in such application areas, the why is often more important than a standard AI result per se. Consequently, both explainability and robustness can promote trust and reliability and ensure human sustainability that combines human intelligence with artificial intelligence.

Quick Start

As a quick start you can do two steps before delving into details:
1) You can read this introduction:
Holzinger, A. 2016. Machine Learning for Health Informatics. In: Holzinger, A. (ed.) Machine Learning for Health Informatics: State-of-the-Art and Future Challenges. Cham: Springer International Publishing, pp. 1-24, doi:10.1007/978-3-319-50478-0_1. [pdf], and

2) You can watch this introduction video on Youtube:
https://www.youtube.com/watch?v=lc2hvuh0FwQ

3) And you can make yourself familiar with the health informatics domain:
https://www.springer.com/de/book/9783319045276

Please always keep in mind: Machine learning for health informatics needs an integrative approach: algorithm development is at the core, however, 70% of the work is in data preprocessing, data mapping, data fusion; and at the end of the day you have a “customer”, which means that you have to visualize your results gained in arbitrarily high dimensional spaces into the lower dimension, which means  to map it from RN to R2 – which is a diffcult task.

REMEMBER: Machine learning needs top-quality data !

There are many excellent textbooks in machine learning, but if I would be forced to give a maximum of three recommendations – I would take my three favourites:

The magical number three and my personal recommendation is to read it in this order:

1) Start with Chris BISHOP (2006) Pattern Recognition and Machine Learning, Springer,
2) Delve into Kevin MURPHY (2012) Machine Learning: A Probabilistic Perspective, MIT Press, and
3) Explore newest trends with Ian GOODFELLOW, Yoshua BENGIO & Aaron COURVILLE (2016) Deep Learning, MIT Press.

Those three are my favourite textbooks (in German “Lieblingsbücher”), Nr. 3 is named “Deep Learning” but it shows impressively that deep learning is much more than only neural networks (in German “Depp Learning”), but with many facets, awesome and super interesting!

In my machine learning course LV185.A83 crossreferences are provided with the following shortcuts: [BIS-ppp], [MUR-ppp] and [GBC-ppp].

Here some more suggestions (I apologize for the incompleteness)

  • Tom M. MITCHELL (1997). Machine learning, New York: McGraw Hill.  (Book Webpages)
    Undoubtedly, this is the (!) classic source from the pioneer of ML, for getting a perfect first contact with the fascinating field of ML, for undergraduate and graduate students, and for developers and researchers. No previous background in artificial intelligence or statistics is required.
  • Peter FLACH (2012). Machine Learning: The Art and Science of Algorithms that Make Sense of Data. Cambridge: Cambridge University Press. (Book Webpages)
    Introductory for advanced undergraduate or graduate students, at the same time aiming at interested academics and professionals with a background in neighbouring disciplines. It includes necessary mathematical details, but emphasizes on how-to. Very good read and handy on the desk for quick reference.
  • Trevor HASTIE, Robert TIBSHIRANI, Jerome FRIEDMAN (2009). The Elements of Statistical Learning: Data Mining, Inference, and Prediction. New York: Springer-Verlag (Book Webpages). This is the classic groundwork from supervised to unsupervised learning, with many applications in medicine, biology, finance, and marketing. For advanced undergraduates and graduates with some mathematical interest.
  • David BARBER (2012). Bayesian Reasoning and Machine Learning. Cambridge: Cambridge University Press. (Book Webpages). Online Version available thanks to the Publisher. Great book for computer science students with modest mathematical background – for undergraduates and master’s students. Comprehensive and coherent, it develops the essentials from reasoning to advanced techniques within the framework of graphical models. Students learn more than a menu of techniques, they develop analytical and problem-solving skills that equip them for the real world. Only disadvantage is IMHO that it fosters MATLAB.
  • Carl E. RASMUSSEN & Christopher K.I. WILLIAMS (2006). Gaussian Processes for Machine Learning. Cambridge: MIT Press. (Book Homepage)
    GPs have meanwhile received the necessary attention among the machine learning community, and this book provides the systematic study of theoretical and practical aspects of GPs in machine learning.  Many connections to other well-known techniques from machine learning and statistics are discussed, including support-vector machines, neural networks, splines, regularization networks, relevance vector machines and others. Theoretical issues including learning curves and the PAC-Bayesian framework are treated, and several approximation methods for learning with large datasets are discussed. The books provides excellent mathematical background.

And here some suggestions to get an understanding of the complexity of the health informatics domain:

  • Andreas HOLZINGER, 2014. Biomedical Informatics: Discovering Knowledge in Big Data.
    New York: Springer. (Book Webpage)
    This is a students textbook for undergraduates, and graduate students in health informatics, biomedical engineering, telematics or software engineering with an interest in knowledge discovery. This book fosters an integrated approach, i.e. in the health sciences, a comprehensive and overarching overview of the data science ecosystem and knowledge discovery pipeline is essential.
  • Gregory A PETSKO & Dagmar RINGE, 2009. Protein Structure and Function (Primers in Biology). Oxford: Oxford University Press (Book Webpage)
    This is a comprehensive introduction into the building blocks of life, a beautiful book without ballast. It starts with the consideration of the link between protein sequence and structure, and continues to explore the structural basis of protein functions and how this functions are controlled.
  • Ingvar EIDHAMMER, Inge JONASSEN, William R TAYLOR, 2004. Protein Bioinformatics: An Algorithmic Approach to Sequence and Structure Analysis. Chicheser: Wiley.
    Bioinformatics is the study of biological information and biological systems – such as of the relationships between the sequence, structure and function of genes and proteins. The subject has seen tremendous development in recent years, and there are ever-increasing needs for good understanding of quantitative methods in the study of proteins. This book takes the novel approach of covering both the sequence and structure analysis of proteins and from an algorithmic perspective.

Glossary

Dimension = n attributes which jointly describe a property. Examples for high dimensional data sets are omics data (e.g. genomics, proteomics, metabolomics).

Features = any measurements, attributes or traits representing the data. Features are key for learning and understanding. a synonym for feature is dimension, due to the fact that an data object with n features can be represented as a n-dimensional point in an n-dimensional space by a feature vector. A main challenge therefore is in dimensionality reduction, which is the process of mapping an n-dimensional point, into a lower k-dimensional space – which is one task of visualization (see area 6 in the HCI-KDD pipeline).

Function learning = understanding relationships between continuous variables, e.g. learning how hard to press the gas pedal for a certain acceleration of a car. There are two approaches: rule-based polynomials or power-law functions; and similarity-based theories which focus on the idea that humans learn by forming associations: if x is used to predict y, observations with similar x values should also have similar y values (refer to the work around Thomas L. GRIFFITHS, Psychology, Berkeley); in machine learning this is a hard task, see e.g. Auer, P., Long, P. M., Maass, W. & Woeginger, G. J. 1995. On the complexity of function learning. Machine Learning, 18, (2-3), 187-230, doi:10.1007/BF00993410.

Gaussian Process GP = defines a prior over functions, which can be converted to a posterior over functions after learning some data [MUR-515]. Generally, GPs are nonparametric Bayesian models, where observations occur in a continuous domain, e.g. in time or space. In a GP every point in some continuous input space is associated with a normally distributed random variable. Moreover, every finite collection of those random variables has a multivariate normal distribution. For ML essential is the fact that the distribution of a GP is the joint distribution of all those (infinitely many) random variables, and as such, it is a distribution over functions with a continuous domain, again in time or space.

Kernel function = defined as a real-valued function of two arguments,

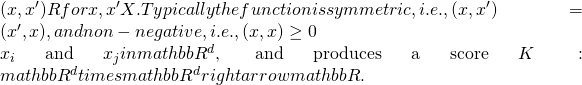κ (x, x') ∈ R for x, x' ∈ X. Typically the function is symmetric, i.e., κ (x, x') = κ (x', x), and non-negative, i.e., κ (x, x) \ge 0 $x_{i}$ and $x_{j} in mathbb{R}^{d}$, and produces a score $K: mathbb{R}^{d} times mathbb{R}^{d} rightarrow mathbb{R}$. , so it can be interpreted as a measure of similarity [MUR:479-513].

Human kernel =  is a function which can also be provided by a human to the machine learning algorithm, thus: human kernel. Automatically, this is done by the Support Vector Machine (SVM), because under certain conditions a kernel can be represented by a dot product in a high-dimensional space (Mercer’s theorem).

Reals = numbers expressible as finite/infinite decimals

Regression = predicting the value of a random variable y from a measurement x.

Reinforcement learning = adaptive control, i.e. to learn how to (re-)act in a given environment, given delayed/ nondeterministic rewards.  Human learning is mostly reinforcement learning.

On Algorithms

Jason BROWNLEE (2012). Clever Algorithms: Nature-Inspired Programming Recipes, Online available

Robert SEDGEWICK & Kevin WAYNE (2011). Algorithms, 4th Edition. Upper Saddle River (NJ): Pearson. Online Material

On Machine Learning

Trevor HASTIE, Robert TIBSHIRANI & Jerome FRIEDMAN (2011). The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Second Edition. New York: Springer > Online material  > Video Lecture

Jure LESKOVEC, Anand RAJARAMAN, Jeff ULLMAN (2014). Mning of Massive Datasets. Second Edition. Cambridge University Press > Online material > Video lectures

Video Lectures

SIGKDD > 20th ACM SIGKDD Conference on Knowledge Discovery and Data Mining (KDD), New York,  August 24-27, 2014 > KDD 2014 Videolectures

Open Data Sets

Nature Scientific Data is a recently launched open-access, online-only journal for openly accessible scientific data from all disciplines. The articles are called Data Descriptors, combine traditional narrative content with curated descriptions of research data to support reproducibility, as this may accelerate scientific discovery:
https://www.nature.com/sdata/

Goudiaby, V., Zuidema, P. A. & Mohren, G. M. J. 2014. Data storage: Overcome hurdles to global databases. Nature, 511, (7510), 410-410.

Editorial to Nature Volume 515, Issue 7527 > Data-access practices strengthened

Mathematical Background

Springer Open Access Encyclopedia of Mathematics https://www.encyclopediaofmath.org

Chang, L. A. (1983) Handbook for Spoken Mathematics (Larry’s Speakeasy) > Barrier free resource

Free Online Mathematics Reference work by Eric W. Weisstein > Wolfram MathWorld

Useful hints for reading mathematical expressions in English > Saying Maths

Simovici, D. A. & Djeraba, C. 2014. Mathematical Tools for Data Mining: Set Theory, Partial Orders, Combinatorics, London, Heidelberg, New York, Dordrecht, Springer. [10.1007/978-1-4471-6407-4]

Basic Science

The top 100 most cited papers: Nature explores the most-cited research of all times, unbeaten Nr. 1 is Lowry, O. H., Rosebrough, N. J., Farr, A. L. & Randall, R. J. 1951. Protein measurement with the Folin phenol reagent. J biol Chem, 193, (1), 265-275 with 350.000+ citations; amongst the top 100 are papers from Bioinformatics, Biology lab techniques, Crystallography, Mathematics, Statistics, Medical statistics, Medicine, Phylogenetics, Physical chemistry, Physics and Psychology.
https://www.nature.com/news/the-top-100-papers-1.16224

Turing, A. M. 1937. On computable numbers, with an application to the Entscheidungsproblem. Proceedings of the London Mathematical Society, 42, (1), 230-265. [10.1112/plms/s2-42.1.230]